
代码如下:
function print(v){
if (typeof v == "number") {
var w = 30
if(n>30) w = (n-30) + 40
var s = '<span style="padding:4px 2pxdisplay:inline-blocktext-align:centerwidth:' + w + 'px">'+v+'</span>'
document.write(s)
}else{
document.write(v)
}
}
var n = prompt("请输入幂数:",9)
n = n - 0
var t1 = new Date()
var a1 = [1,1]
var a2 = [1,1]
print('<div style=text-align:center">')
for (var i = 0i <=ni++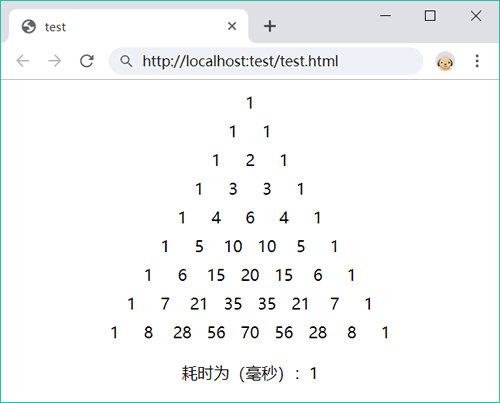){
for (var j = 1j <i + 2j++) {
print(c(i,j))
}
print("<br />")
}
print("</div>")
var t2 = new Date()
print("<p style='text-align:center'>耗时为(毫秒):"+(t2-t1)+"</p>")
function c(x,y){
if ((y == 1) || (y == x + 1)) return 1
return c(x-1,y-1) + c(x-1,y)
}
扩展资料
杨辉三角的特点:
1、每个数等于它上方两数之和。
2、每行数字左右对称,由1开始逐渐变大。
3、第n行的数字有n项。
4、前n行共[(1+n)n]/2 个数。
5、第n行的m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
6、第n行的第m个数和第n-m+1个数相等 ,为组合数性质之一。
7、每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和,这也是组合数的性质之一。
先上效果图:
代码如下:
function pTriangle(){
let output = []
for(let i=0i<10i++){
let a = []
for(let j=0j<10j++){
if(j===0||j===i){
//第0列和对角线为1
a[j] = 1
}else if(j>i){
//上三角元素为0
a[j]=0
}else{
a[j] = output[i-1][j-1]+output[i-1][j]
}
}
output[i]=a
}
console.info(output)
}
pTriangle()
如果帮助到你的话,请点个采纳+赞哦,感谢。
代码:
#include<stdio.h>
#define N 10
void setdata(int(*s)[N],int n){
int i,j
for(i=0i<ni++)//第一列和对角线上的元素都置1
{
s<i><i>=1s<i>[0]=1
}
for(i=2i<ni++){//给杨辉三角形其他元素置数
for(j=1j<ij++){
s<i>[j]=s[i-1][j-1]+s[i-1][j]
}
}
}
void outdata(int s[][N],int n){
int i,j
printf("杨辉三角形:\n")//只输出矩阵下半三角
for(i=0i<ni++){
for(j=0j<=ij++){
printf("%6d",s<i>[j])
}
printf("\n")
}
}
main(){
int y[N][N],n=7
setdata(y,n)//按规律给数组元素置数
outdata(y,n)//输出杨辉三角形
}
可以将杨辉三角形的值放在一个方形矩阵的下半三角中,如需打印7行杨辉三角形,应该定义等于或大于7x7的方形矩阵,只是矩阵的上半部分和其余部分并不使用。
杨辉三角形具有以下特点:
(1)第一列和对角线上的元素都为1;
(2)除第一列和对角线上的元素之外,其他的元素的值均为前一行上的同列元素和前一列元素之和。
方法二、
#include<stdio.h>
#define LINE 10
int main()
{
int arr[LINE][LINE]={0}
int i=0
int j=0
for(i=0i<LINEi++)
{
arr<i>[0]=1
arr<i><i>=1
}
for(i=2i<LINEi++)
{
for(j=1j<ij++)
{
arr<i>[j]=arr[i-1][j-1]+arr[i-1][j]
}
}
for(i=0i<LINEi++)
{
for(j=0j<(2*LINE-2*i)j++)
{
printf("")
}
for(j=0j<=ij++)
{
printf("%4d",arr<i>[j])
}
printf("\n")
}
return 0
}
方法三、
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int main()
{
int i,j,n=0
//首先定义二维数组计数符号i,j还有杨辉三角行数的初始化
int a[100][100]={0,1}
//只有2个初值,即a[0][0]=1,a[0][1]=2,其余数组元素的初值均为0
//二维数组大小可自定,但切记不可使其超过整形数组的大小
while(n<1||n>100)
//在输入的值不正确时自动初始化问题,重新输入
{
printf("请输入要打印的杨辉三角行数>:")
scanf("%d",&n)
}
for(i=1i<ni++)//第一层循环i决定第几行
{
for(j=1j<=ij++)//第二层循环借用i限制每行字符数目
{
a<i>[j]=a[i-1][j-1]+a[i-1][j]
}
}
for(i=1i<ni++)//一个for循环逐行打印叫a的二维数组
{
for(j=1j<=ij++)
printf("%5d",a<i>[j])
printf("\n")
}
return 0





































































