2. threejs源码阅读——mathmatrix

JavaScript014

2. threejs源码阅读——mathmatrix,第1张

与 Vector接口 一样，threejs也在 Matrix3.d.ts 文件中提供了一个 Matrix 接口，并且在 Matrix3 （3x3矩阵类）和 Maxtrix4 （4x4矩阵类）中实现了该接口。

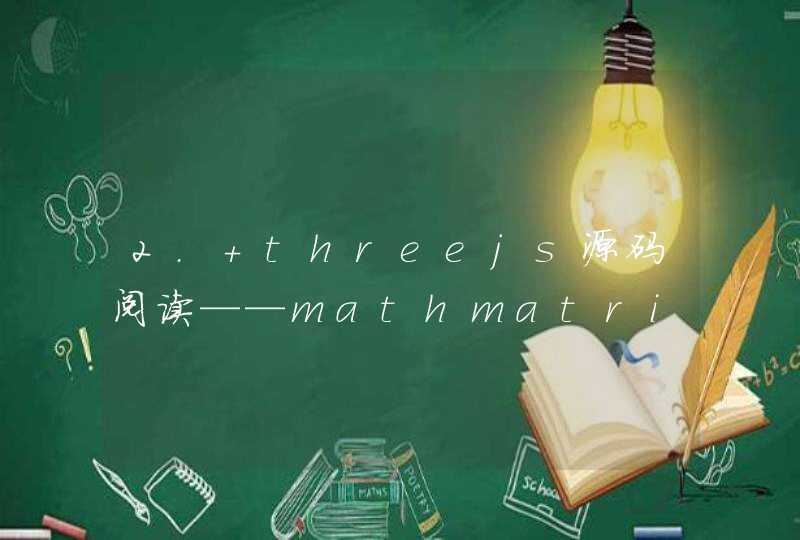
我们可以看到，矩阵中的元素是用数组的方式储存的。由于不同维度的矩阵内所用的元素个数不同，所以Matrix3和Matrix4的set方法是分开声明在每个类中的。这里我们以Matrix3.set为例：

可以看到，在set时是以行优先的顺序进行传值的，也就是第一行第一个，第一行第二个，第一行第三个，第二行第一个，第二行第二个...

但是在set方法的实现中，可以看到elements数组内是以列优先的顺序进行存储的：

简单点说，这里只是 存储方式的不同 。由于大多数人都习惯以行优先的方式考虑矩阵，所以threejs中所有的文档都是以行优先的方式表示的。但如果我们想要阅读源码，就要注意到[n11, n12, n13, n21 ... n33]并不是按顺序储存在elements中。事实上如果我们按顺序读取elements中的元素并以行优先的方式组成矩阵，它将是原本矩阵的转置矩阵。

如同Vector的类型，Matrix类型中所有返回值为自身类对象的方法也是原地修改该对象。例如 Transpose转置

所有的Matrix也提供了clone和copy方法，用于深拷贝不同Matrix对象。

那么threejs中的向量与矩阵进行计算是以什么形式进行的呢？这里我们举一个例子。

在Vector3类中提供了appyMatrix3这个方法，这个方法以一个3x3的矩阵作为参数，相乘后原地修改向量的值。

如果我们将Vector3看做 三行一列的矩阵（3x1） 的话，那么就需要左乘3x3矩阵，最后得到列向量：

如果我们将Vecot3看做 一行三列的矩阵（1x3） 的话，那么就需要右乘3x3矩阵，最后得到行向量：

接下来，我们再假设一个向量

加入齐次坐标w=1，来表示三维空间中的一个点（1,2,3）

然后我们构建一个仿射变换矩阵做缩放+平移运算

即沿着xyz轴均缩放2倍，然后沿着xyz移动5个单位距离。最终结果是：

这个计算我们会使用Vector3.applyMatrix4

接下来验证一下：

控制台打印结果：

threejs中的矩阵以 行优先 的形式初始化，以 列优先 的形式储存。

threejs中的向量采用 列向量 ，与矩阵做 左乘运算 。

threejs中一个三维向量与4x4的矩阵进行运算时，会先给三维向量补充第四个值w，也就是齐次坐标，w值与矩阵的第四行有关系：

在上面的例子中，我们使用了一个缩放+平移的 仿射变换矩阵 作为例子，此时w为1。

从Git上Clone好项目后，目录结构如下：

src - 我们主要看的部分，包含了所有源码。

editor - 如果有自己做webgl webIDE的计划，可以参考一下。threejs的IDE多少年没变过了，功能很少也不太好用。

docs - 所有的教程和api文档，文件夹内有index页面可以直接本地浏览，比较方便，省的连外网了。

examples - 所有示例的源码，每个html文件的名字就是示例的名字，可以直接在本地运行。

build - 打包后的源码，一个是按module加载的，一个是整体加载的。

threejs源码中的每个类几乎都有2个文件。一个是ts文件，用来声明方法和变量，一个是js文件，用来实现。最终在打包输出的时候，都会被编译成js语法。

在本系列文章中，我们重点解读js文件中的内容，ts文件中的声明内容作为辅助，帮助我们理解每个js文件的大结构和功能。

可能很多同学会发现，学习Three.js的API非常容易，但是真正理解API的作用却非常难。其实让大家感到难的并不是Three.js本身，而是Three.js背后所隐藏的3D图形学知识。本系列Three.js源码解读文章，会帮你一边补齐3D图形学的基础知识，一边真正理解到Three.js的实现原理，知其然，知其所以然。

Object3D是ThreeJS中大部分物体的基类，它包含了物体的位移，旋转，缩放，以及各个物体父子关系的js实现。选取Object3D几个重要的属性做解释：

一个3D对象往往由多个父子对象组成，父对象的位移, 旋转, 缩放会传递给所有的子对象。

this.parent指向父对象，this.children包含了所有的子对象。

通过 add 为物体添加子对象。需要注意的是，如果该子对象有其他的父对象，会先解除子对象和旧的父对象的父子关系，然后将子对象添加到新的父对象中。

this.matrix表示物体自身的本地形变，this.matrixWorld表示物体的全局形变。当物体没有父对象时，全局形变就是本地形变。

为什么对象组合这么重要呢？看下面的例子：

这两个立方体共同组成了一个3D对象，下面的立方体为底座，上面的立方体为操作臂。当底座转动的时候，操作臂会同样转动，所以操作臂的形变会传递给底座。当操作臂旋转时，底座不会被影响。

这里，底座就是操作臂的父对象。只要简单的将底座的全局形变(this.parent.matrixWorld)和操作臂的本地形变(this.matrix)相乘，就能得到操作臂的最终形变。是不是很方便？

3D物体的位移，旋转，缩放都可以通过矩阵表示。其中，旋转除了通过矩阵，还可以通过欧拉角和四元数表示。

Object3D的rotation代表物体旋转的欧拉角表示，quaternion代表了四元数表示，他们是3D物体统一旋转的不同数学表达方式。(矩阵，欧拉角，四元数表示旋转

onRotationChange , onQuaternionChange 这两个回调用于同步欧拉角和四元数，保证他们代表着相同的旋转角度。

3D交互一个很大一部分工作量是需要在物体的本地空间( this.matrix )和世界空间( this.matrixWorld )进行坐标转换。