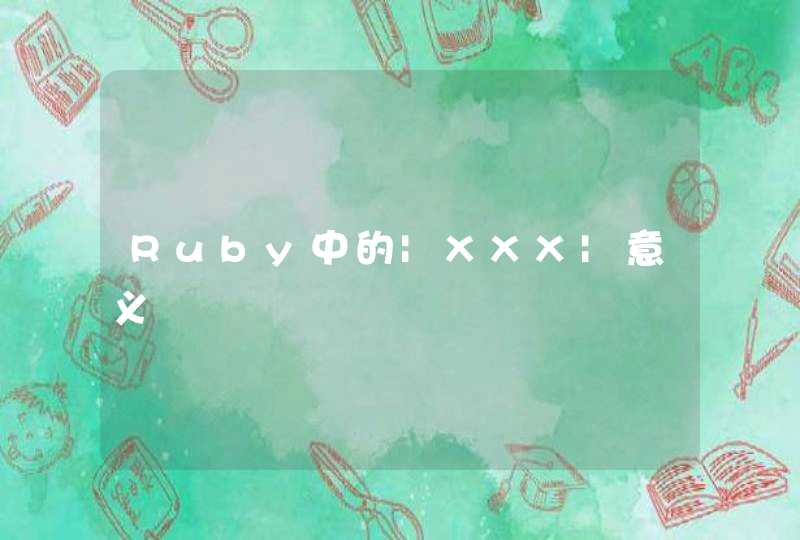你也可以算出圆周率的 - 随机落点算法 - 致即将到来的圆周率日

Python020

你也可以算出圆周率的 - 随机落点算法 - 致即将到来的圆周率日,第1张

一年一度的圆周率日就要到了，是的，就是3月14日，因为它与圆周率π的前几位3.14的数字一样。

我们知道，传说中祖冲之计算圆周率用的是“割圆术”的改进方法，可惜我们大多数现代人的脑子已经无法理解这种方法了。使用其他的复杂公式也有，但人的脑子更不容易理解，但有一个异想天开的方法你知道吗？任何人可以简单地去计算出Pi呢（下面我们都用Pi来代替圆周率π吧，好写好认，：p）。

这个方法源自概率论的基础，叫做蒙特卡洛法，形象一点的话我们也可以把它称为随机落点法，我们先说说它的原理：

我们先看看下面这张图

假设有图中的一个正方形和一个刚好套在它中间的圆形，可以很直观地看出：圆形的半径如果是R的话，正方形的边长就是2R。

圆形的面积根据公式是Pi乘以R的平方，也就是 Pi × R × R = PiR²

正方形的面积根据公式是边长的平方，也就是（2R）×（2R）= 4R²

把两个式子相除一下，可以很容易地推算出来，Pi = （圆形的面积 ÷ 正方形的面积）× 4

这样，就巧妙地把计算Pi值的问题转换成计算符合上面图中条件的圆形与正方形的面积之比的计算了。

这时候，概率论可以出场发挥作用了，以及有了计算机之后，我们有的“随机数”这个武器！

假设我们随机在正方形范围内画一个点，那么这个点有可能落在圆形之中，也有可能落在圆形之外；然后我们重复这个动作，从概率论上来说，如果进行无限多次，那么落在圆形中的点的个数与所有已经画的点的个数之比，就应该是圆形的面积和正方形的面积之比。看看下面这张图是不是就好理解了？

想想当里面的点数足够多的时候，就可以覆盖满整个原型和正方形。俗话说：“以点带面”，这时候就可以理解成无数多的点组成了圆形和正方形的面积。

好了，那么下面我们看看用计算机程序来实现这种方法计算圆周率的效果吧！我们这次选用Go语言（Golang）来实现这个算法，因为Go语言相对速度较快（比Python和Java等解释型语言要快得多），编写起来又比C语言更容易看懂。

这段程序的运行结果是：

可以看出来，计算出来的圆周率Pi值越来越接近于我们所熟知的数字：3.1415……

神奇吧，为什么说人也可以算出来呢？假想在地上用粉笔画一个那样的正方形和圆形，然后我们随性地往里扔沙包吧！很童真的画面吧？

#include <stdio.h>

#define L 10000 //求10000位PI值

#define N L/4+1

// L 为位数，N是array长度

/*圆周率后的小数位数是无止境的，如何使用电脑来计算这无止境的小数是一些数学家与程式设计师所感兴趣的，在这边介绍一个公式配合 大数运算，可以计算指定位数的圆周率。

John Wallis的圆周率公式：

//详细看网站介绍：https://baike.baidu.com/item/%E5%9C%86%E5%91%A8%E7%8E%87/139930?fr=aladdin

PI = [16/5 - 16 / (3*53) + 16 / (5*55) - 16 / (7*57) + ......] - [4/239 - 4/(3*2393) + 4/(5*2395) - 4/(7*2397) + ......]

*/

void add ( int*, int*, int* )

void sub ( int*, int*, int* )

void div ( int*, int, int* )

int main ( void )

{

int s[N+3] = {0}

int w[N+3] = {0}

int v[N+3] = {0}

int q[N+3] = {0}

int n = ( int ) ( L/1.39793 + 1 )

int k

w[0] = 16*5

v[0] = 4*239

for ( k = 1k <= nk++ )

{

// 套用公式

div ( w, 25, w )

div ( v, 239, v )

div ( v, 239, v )

sub ( w, v, q )

div ( q, 2*k-1, q )

if ( k%2 ) // 奇数项

add ( s, q, s )

else// 偶数项

sub ( s, q, s )

}

printf ( "%d.", s[0] )

for ( k = 1k <Nk++ )

printf ( "%04d", s[k] )

printf ( "\n" )

return 0

}

void add ( int *a, int *b, int *c )

{

int i, carry = 0

for ( i = N+1i >= 0i-- )

{

c[i] = a[i] + b[i] + carry

if ( c[i] <10000 )

carry = 0

else // 进位

{

c[i] = c[i] - 10000

carry = 1

}

}

}

void sub ( int *a, int *b, int *c )

{

int i, borrow = 0

for ( i = N+1i >= 0i-- )

{

c[i] = a[i] - b[i] - borrow

if ( c[i] >= 0 )

borrow = 0

else // 借位

{

c[i] = c[i] + 10000

borrow = 1

}

}

}

void div ( int *a, int b, int *c ) // b 为除数

{

int i, tmp, remain = 0

for ( i = 0i <= N+1i++ )

{

tmp = a[i] + remain

c[i] = tmp / b

remain = ( tmp % b ) * 10000

}

}

le-7改成1e-7，是数字1，不是字母l。

pi的近似计算公式是pi=4*(1-1/3+1/5-1/7+...)，所以上述注释为：

while((fabs(t))>le-7)// 如果1/n小于1e-7，则停止计算。

{ pi=pi+t // 对照近似计算公式

n=n+2 // 对照近似计算公式

s=-s // s是用来交替变化+、-号的

t=s/n // 对照近似计算公式

}

pi=pi*4// 对照近似计算公式