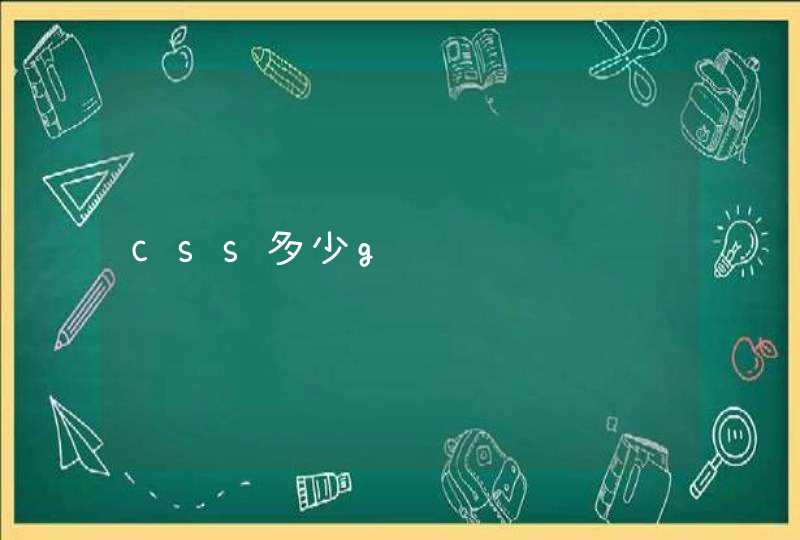输入节点,然后分别建底下的各个孩子,注意,每个孩子都要求输入数据,没有则输入0.反正建树很烦
#include <stdio.h>
#include <malloc.h>
#include <math.h>
#include <conio.h>
#define MAX_DEPTH 4
#define MAX_CHILDREN_NUM 3 //三叉树
typedef struct tnode
{
int data
tnode **children, *parent//parent域可不要
}tnode
typedefstruct
{
tnode* ptr
int cur//cur记录当前访问到的孩子节点下标
bool visited//是否被访问标记
}snode
typedef struct
{
snode *elem
int top
}stack
void initstack(stack *s)
{
s->elem=(snode*)malloc(
(int)pow(MAX_CHILDREN_NUM,MAX_DEPTH)*sizeof(snode))
s->top = 0
}
void pop(stack *s, snode *e)
{
--s->top
*e = s->elem[s->top]
}
void push(stack *s, snode *e)
{
s->elem[s->top] = *e
++s->top
}
void create(tnode **t, tnode *parent)
{
int n
scanf("%d", &n)
if(!n)
{
*t = NULL
return
}
else
{
*t = (tnode*)malloc(sizeof(tnode))
(*t)->data = n
(*t)->parent = parent//可不要
(*t)->children = (tnode**)malloc(MAX_CHILDREN_NUM*sizeof(tnode*))
for(n = 0n <MAX_CHILDREN_NUM++n)
create(&(*t)->children[n], *t)
}
}
void visit(tnode *t)
{
printf("%5d", t->data)
}
void postorder1(tnode *t)
{
int i
if(t)
{
for(i = 0i <MAX_CHILDREN_NUM++i)
postorder1(t->children[i])
visit(t)
}
}
void postorder2(tnode *t)
{// 和前序遍历基本相同,只是把访问语句的执行由
// 入栈时执行改为出栈时执行
stack s
snode e
initstack(&s)
e.ptr = t
e.cur = 0
e.visited = false
push(&s, &e)
while(s.top)
{
while(s.elem[s.top-1].ptr)
{
do
{
e.ptr = s.elem[s.top-1].ptr->children[s.elem[s.top-1].cur]
++s.elem[s.top-1].cur
}while(!e.ptr &&s.elem[s.top-1].cur<MAX_CHILDREN_NUM)
e.cur = 0
e.visited = false
push(&s, &e)
}
pop(&s,&e)
while(s.top &&s.elem[s.top-1].cur == MAX_CHILDREN_NUM)
{
if(!s.elem[s.top-1].visited)
{
visit(s.elem[s.top-1].ptr)
s.elem[s.top-1].visited = true
}
pop(&s, &e)
}
}
}
void main()
{
tnode *T
create(&T, NULL)
printf("\n递归后序遍历:")
postorder1(T)
printf("\n非递归后序遍历:")
postorder2(T)
}
三叉树。准备一点说,是固定子树的多叉树。
比如ID由1到500000之间的50万个元素成员。那么可以建子树为10的多叉树。
stucrt treeten
{
treeten * t_pater
void * DataAdd
unsigned long DataLen
treeten * t_sub0
treeten * t_sub1
treeten * t_sub2
treeten * t_sub3
treeten * t_sub4
treeten * t_sub5
treeten * t_sub6
treeten * t_sub7
treeten * t_sub8
treeten * t_sub9
}//占用52字节.
ID上限50万(500000是6位数),需五层树结构,每一层树会产生10个子树,5层树是10的6次方减1个树(含根树)。每个树占用52字节,共约需内存50MB.
ID为123456的成员所在树的位置:
根树中:t_sub1.
第一层子树:t_sub2.
第二层子树:t_sub3.
第三层子树:t_sub4.
第四层子树:t_sub5.
第五层子树:t_sub6.
读取第五层子树t_sub6指向的第六层子树的DataAdd和DataLen记录进行数据读取操作.
同理,ID为500000的成员所在树的位置是
根树:t_sub5
第一层子树:t_sub0.
第二层子树:t_sub0.
第三层子树:t_sub0.
第四层子树:t_sub0.
第五层子树:t_sub0.
读取第五层子树t_sub0指向的第六层子树的DataAdd和DataLen记录进行数据读取操作.
所有ID在整个树的结构中位置是唯一的。也就是基于ID的树结构算法。
即,查找一个数字长度为6的ID成员,只需要重复7次操作,远远高于链表速度。但内存开支远远大于链表,即限制了树的结构层数,因为这是以指数形式增涨开支内存的。
这是查找和读取操作。
添加相对于删除要简单一点。跟查找相近,一层一层找下一层子树的保存地址。没有,就申请,循环到最后一层。然后保存数据。
删除,最麻烦的事,如果删除的是树的最后一层,那么可以直接删除,如果被删除的树还有子树,就需要遍历该树下所有子树进行删除,否则内存泄漏。
总结,三叉树用来解决大量元素的操作时,速度上优于其他方法。但树的成员越多,层数越多,内存开支会非常庞大。
我最近在做一个支持64位的树操作,基于文件的,打算支持10层字符串查找(字符:A-Z,0-9,即36个子树)也就是约36的10次方个字节,内存无法满足,但基值小于2的64次方,所以可基于文件进行操作。
参考下。算法可能不是最佳的,交流经验为主哈。